[데이터분석 공부 3일차] 확률과 확률분포

확률이란?

경험 혹은 실험의 결과로 특정한 사건이나 결과가 발생할 가능성

표본 공간(S)에서의 임의 사건(E)에 대해서 사건이 발생할 확률(P)은 아래의 세 조건을 만족해야 함

• $$ 0 \leq P(E) \leq 1 $$
• $$ P(S) = 1 $$
• $$ E_1, E_2, \dots $$ 이 서로 배반사건일 때 $$P(\bigcup_{i=1}^{\infty}E_i) =  \sum_{i=1}^{\infty}P(E_i) $$

 

• 표본공간(sample space) : 통계적 실험에서 모든 가능한 결과의 집합
• 사건(event) : 관심이 있는 실험 결과의 집합(표본 공간의 부분 집합)
• 근원사건 : 한 개의 원소로 된 사건

 

사건의 연산

• 합사건 : $$ A \cup B $$
• 곱사건 : $$ A \cap B $$
• 여사건 : $$ A^c $$
• 배반사건 : $$ A \cap B = \text{\O} $$

조건부 확률

사건 B ( P(B)>0, B가 일어날 확률이 0보다 클 때)가 발생한 상태에서 사건 A가 일어날 확률

$$\text{If}\enspace P(B) > 0, then \enspace P(A\text{\textbar}B)= \dfrac{P(A \cap B )}{P(B)} $$

 

확률의 특성

• 합사건 :$$ P(A \cup B) = P(A) + P(B) - P(A \cap B)$$
• 곱셈법칙 :$$ P(A\text{\textbar}B)=P(A\text{\textbar}B) \cdot P(B) = P(B\text{\textbar}A) \cdot P(A)$$
• 여사건 :$$ P(A^c) = 1 - P(A) $$
• 독립사건: $$P(A \cap B) = P(A)P(B) , P(A \text{\textbar} B) = P(A), P(B \text{\textbar} A) = P(B) $$
• 덧셈정리: $$P(A \cap B) = P(A)P(B \text{\textbar} A) = P(B)P(A \text{\textbar} B) $$

베이즈 정리(Bay's Theorem)

조건부 확률을 이용해 사전 확률과 사후 확률의 관계를 추정하는 정리

어떤 사건이 발생할 확률을 객관적인 정보를 확보하였을 때,  정교화하는데 활용함.

 

• 사전확률(Prior probability) : A라는 사건의 발생 확률 P(A)
• 사후확률(Posterior probability) : B라는 사건이 주어졌을 때 A의 발생 확률 P(A|B)

P(B) = P(B∩A)

= P(B∩A1) + P(B∩A2)

= P(B|A1)P(A1) + P(B|A2)P(A2)

 

 

확률변수

표본공긴(S) 내의 각 사건들에 실수 값을 대응시키는 함수

사건의 발생에 따라 각각 다른 확률 값을 가짐

 

• 연속형 확률 변수 : 확률 변수 X가 구간 또는 구간들의 모임인 숫자 값을 갖고, 확률 분포함수로 확률 밀도 함수를 가짐
• 이상형 확률 변수 : 확률 변수 X가 값이 지정된 유한 범위 또는 셀 수 있는 목록 중 하나의 값을 가지고, 확률 분포 함수로 확률 질량 함수를 가짐
• 확률질량함수 : 이산형 확률 변수를 X라고 할 때, X가 취하는 특정 값의 상대적 발생 가능성을 나타내는 함수 
  • ex) 주사위를 한 번 굴릴 때의 값을 나타내는 확률 변수가 X일 때, 이 확률 변수에 대응하는 확률 질량 함수는 Fx(X)=1/6이다.
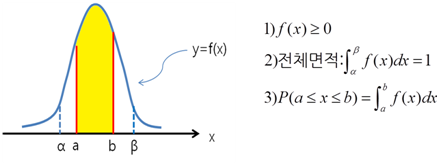
• 확률밀도함수 : 연속형 확률변수를 X라고 할 때, X가 취하는 특정 값의 상대적 발생 가능성을 나타내는 함수 
  • ex) 정규분포 밀도함수

 

 

확률분포의 표준화

확률 변수 X가 평균 A 표준편차 B를 갖는 정규분포를 따를 때, X를 Z = (X-평균)/표준편차를 하면 Z는 표준 정규분포를 갖는 확률 변수가 된다.

 

누적 분포 함수

각 실수 a마다 확률변수 X가 a이하의 값을 취할 확률을 나타내는 함수. 즉 누적 분포 함수를 F라 하면 F(a) = P( X ≤ a)

 

누적 분포 함수의 특성

$$ P(a \lt X \leq b) = F(b) - f(a) $$

$$ F(b)는 b의 증가함수 $$

$$ \lim\nolimits_{b \longrightarrow \infty} F(B) = F(\infty) = 1$$

$$ \lim\nolimits_{b \longrightarrow -\infty} F(B) = F(-\infty) = 0 $$

 

 

 

누적분포함수의 활용

• 주어진 확률변수의 정규분포 여부 검정
• 주어진 확률 변수의 누적 분포 함수와 정규분포의 누적 분포 함수의 일치성을 위한 검정

중심 극한 정리 (Central Limit Theorem)

동일한 확률 분포를 가진 독립 확률 변수 n개의 평균 값들의 분포는 n이 충분히 크다면 정규분포에 가까워진다는 정리

참고 : https://ko.wikipedia.org/wiki/중심_극한_정리

중심 극한 정리 - 위키백과, 우리 모두의 백과사전